1 – INTRODUÇÃO
Na PARTE I do nosso estudo, abordei as diferenças entre os conceitos de alta energia e alta velocidade, demonstrando que dois calibres podem ter a mesma energia e características completamente diferentes. Você viu que a energia é uma grandeza escalar e a velocidade uma grandeza vetorial e percebeu como isso se relaciona ao comportamento do projétil. Nessa segunda parte vamos abordar os aspectos relacionados à balística externa dos ditos “calibres de alta energia”, comparando, novamente, os dois universos compreendidos na mesma faixa de energia: os calibres cujos projéteis possuem velocidade maior e massa menor e os calibres cujos projéteis possuem velocidade menor e massa maior.
Novamente teremos que lançar mão da física na nossa análise, uma vez que o conceito de energia cinética é um conceito da mecânica clássica. Não obstante, novamente tentarei “amaciar” o conteúdo para torná-lo compreensível mesmo aos leitores que não tem muito traquejo com as ciências exatas!
2 – BALÍSTICA EXTERNA E O COMPORTAMENTO DINÂMICO DOS PROJÉTEIS PROPELIDOS POR ARMAS DE FOGO
2.1 – Forças que atuam sobre o projétil
Qualquer corpo em deslocamento no ar estará sujeito a pelo menos duas forças: a força da gravidade e a resistência do ar. A Força da Gravidade, ou peso[1], depende de dois fatores, que são a massa do corpo e a aceleração da gravidade:

A aceleração da gravidade é a mesma para todos os corpos, com valor aproximado de 9,8 m/s2. A aceleração é a variação da velocidade de um corpo, ou seja, a rapidez com que a velocidade aumenta ou diminui. Se dois corpos possuem a mesma aceleração, sofrerão igual acréscimo na sua velocidade em um mesmo intervalo de tempo. Isso significa dizer que se formos considerar apenas a força da gravidade, dois corpos abandonados da mesma altura sempre caem juntos, ao mesmo tempo, pois a variação da velocidade deles é a mesma, independentemente da massa! Isso só é possível no vácuo, pois quando consideramos um corpo em queda livre na atmosfera, teremos a atuação da força de resistência do ar. Para comprovar o que acabei de comentar, sugiro que você assista ao vídeo abaixo, que mostra um experimento em que algumas penas são abandonadas juntamente com uma bola de boliche em uma câmara de vácuo:
Quando estudamos física na escola sempre fazemos questões “desprezando a resistência do ar”, mas na vida real percebemos que a resistência do ar não é nada desprezível e atua de maneira diferente para objetos diferentes. Na verdade, os principais fatores que interferem na resistência do ar são a densidade e a forma do objeto. Se considerarmos objetos com formatos e densidades próximos, entendemos que a resistência do ar atuará de maneira bastante semelhante nos dois objetos.
Ainda tratando da gravidade, considerando projéteis de calibres diferentes, como por exemplo o .223 Remington e o .454 Casull, faço a seguinte pergunta:
Considerando que seja efetuado um tiro com uma arma em calibre .223 Remington e um tiro com uma arma em calibre .454 Casull, ambos os tiros com os canos à mesma altura e na horizontal, ou seja, paralelos ao solo, qual dos dois projéteis irá tocar o chão primeiro? Para refrescar a sua memória, mostro os dados balísticos dos dois calibres na tabela abaixo:
| Calibre | Velocidade (m/s) | Massa (grains) | Energia (Joules) |
| .223 Remington | 990 | 55 | 1.745 |
| .454 Casull | 548 | 260 | 2.531 |
Se você respondeu que será o de calibre .454 Casull, errou… Se respondeu que será o de calibre .223 Remington, errou também! A resposta é: os dois tocarão o chão AO MESMO TEMPO! Se analisar o que foi explicado antes irá entender! A aceleração da gravidade para os dois projéteis é a mesma. A área e a densidade dos dois é relativamente próxima, de forma que a resistência do ar nos dois casos será semelhante! A velocidade na boca do cano é indiferente, no caso do tiro na horizontal. Se o tiro for com o cano em ângulo, a componente vertical da velocidade do projétil mais rápido fará toda a diferença. O objetivo dessa pergunta foi só demonstrar que a ação da gravidade é a mesma para qualquer calibre de arma de fogo. Você mesmo pode fazer esse teste usando dois projéteis ou duas pedras de massas bem diferentes!
A outra força que atua no projétil em deslocamento no ar já foi comentada. É a resistência do ar, que é diretamente proporcional à velocidade do corpo, ou seja, quanto maior a velocidade, maior é a resistência do ar. Novamente lembrando das aulas de física, que consideravam esse fator nulo, o gráfico mostrado na Figura 1 mostra que na vida real não é nem um pouco desprezível! No caso dos projéteis propelidos por armas de fogo, a resistência do ar é proporcional à velocidade ao quadrado. Veja:
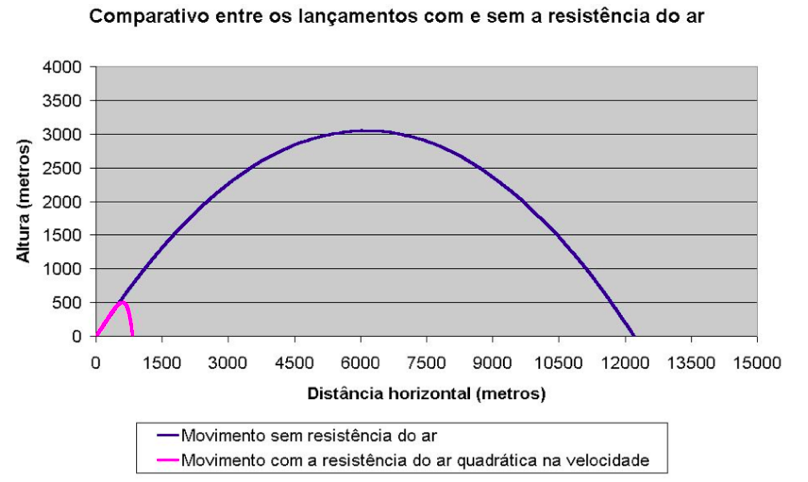
Analisando o gráfico é possível perceber que o alcance do projétil em questão seria de mais de 12 km desprezando a resistência do ar e é de em torno de 750 metros, considerando esse fator, mostrando que não é nada desprezível!
2.2 – A influência do formato do projétil e o coeficiente de arrasto
Como foi visto anteriormente, a aceleração da gravidade imprime aos corpos em queda livre a mesma aceleração, entretanto a velocidade de queda varia de acordo com a resistência do ar, que depende, dentre outros fatores, da forma do corpo que se desloca. Essa dependência do formato do corpo é denominada Coeficiente de Arrasto (Ca). No nosso cotidiano vemos a influência deste coeficiente, seja no formato de um veículo esportivo, de uma ave ou na posição de um ciclista em uma prova de velocidade. Nos três exemplos, percebe-se um formato que tende a ser mais achatado e comprido, conforme se nota na Figura 2:

Figura 2 – Mostra as linhas de escoamento do ar em torno de um automóvel esportivo, um velociclista e uma ave.
Este formato mais alongado produz um arrasto menor pois o ar “desliza” contornando o corpo, produzindo menos turbulência. Nos corpos com formato menos aerodinâmico essa turbulência gera um vácuo atrás do corpo que o “arrasta” no sentido contrário ao movimento, vindo daí o termo Coeficiente de Arrasto[2].
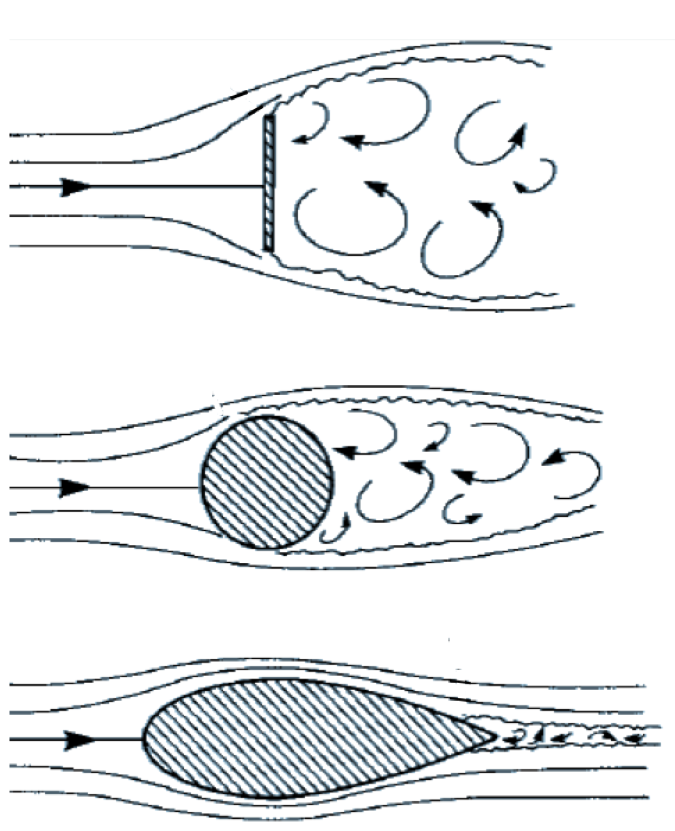
A Figura 4 mostra os Coeficientes de Arrasto de várias geometrias. Quanto maior é o coeficiente, maior é o arrasto gerado no deslocamento do corpo:

É importante destacar que o arrasto e o comportamento do ar em torno do projétil dependem da velocidade de deslocamento dele. Se o projétil é mais lento, o arrasto é menor e o ar consegue contornar mais facilmente o corpo. Em velocidades maiores, o ar tem menos facilidade em contornar o projétil, gerando um arrasto maior. Este tema é brilhantemente tratado pelo colunista Luiz Gaspar no seu livro “Anotações sobre a doutrina policial – Volume 2”, abaixo transcrito:
Quando um projétil se desloca à velocidades subsônicas, o escoamento de ar ao seu redor pode ser considerado incompressível, ou seja, o projétil literalmente empurra o meio ao seu redor de maneira que o ar se desloca e se molda ao escoamento. Esta variação de pressão ocorre até mesmo adiante do projétil (…). Quando tratamos de um regime de velocidade supersônico, o comportamento do meio é modificado. Neste caso, a velocidade do projétil é muito alta para que o ar ao seu redor possa responder a tempo, contornando o projétil. Não há modificação no meio adiante do projétil. Uma vez que o escoamento não pode se adaptar à modificação de pressão, o projétil “colide” com o ar, que é forçado a modificar suas propriedades de pressão, temperatura e densidade, de uma maneira violenta e irreversível, denominada onda de choque. A compressibilidade e a presença de ondas de choque são as principais características de um regime supersônico.
(MARIZ, 2019)
Complementando a explicação de MARIZ(2019), veja a figura Figura 5 da mesma fonte que ilustra a questão:

2.3 – A resistência do ar e o Coeficiente Balístico (CB)
O coeficiente de arrasto é um elemento importante na determinação de como o projétil vencerá a resistência do ar, mas não é o único. Essa facilidade em vencer a resistência do ar é denominada Coeficiente Balístico (CB), que é expresso como se segue:

Como se percebe, o coeficiente balístico relaciona-se à forma, à densidade e ao comprimento do corpo. A dependência da forma já foi explicada anteriormente, quando tratamos sobre o Coeficiente de Arrasto. A densidade está relacionada à inércia do corpo, uma vez que quanto maior for a densidade de um corpo, maior será a massa contida no mesmo volume e, consequentemente, a inércia. A dependência do comprimento do corpo é mais um fator que se relaciona ao formato, uma vez que já foi demonstrado que corpos mais oblongos geram um menor coeficiente de arrasto.
Considerando a relação entre a densidade, massa e dimensões de um corpo, e considerando também que o volume de um corpo com geometria simples é a área dele multiplicada pelo comprimento, é possível transformar a Equação 2 pela substituição expressa na Equação 3:
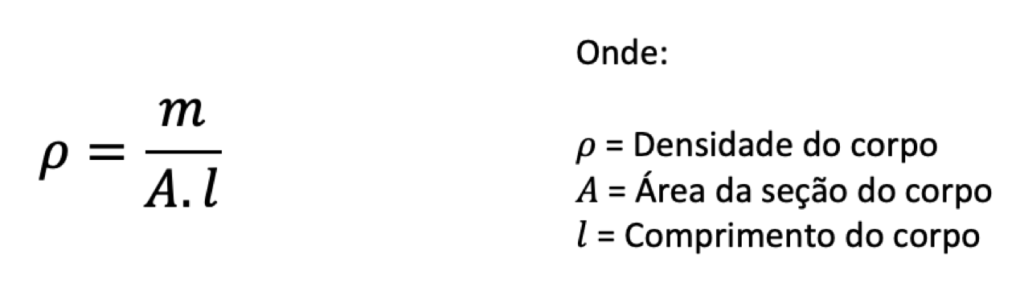
Portanto:
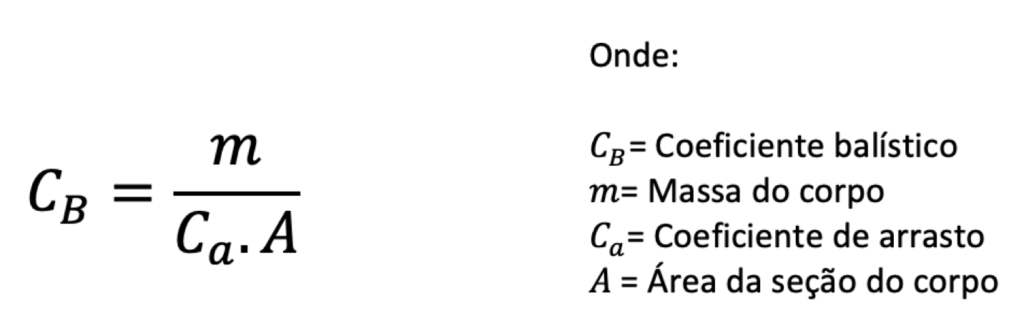
Analisando a Equação 4 percebe-se a contribuição da massa no Coeficiente balístico. Essa contribuição, conforme explicado anteriormente, se deve à maior inércia do corpo, que é a tendência dele se manter no estado de repouso ou movimento em que se encontra. Pode, grosso modo, ser entendida como a dificuldade de parar um corpo em movimento.
Uma outra forma de se entender o Coeficiente Balístico é a capacidade de um corpo manter a sua energia cinética, uma vez que a perda de energia em virtude do atrito do corpo com o ar será menor.
Até o momento é importante que você tenha entendido os conceitos aqui tratados, não só por se relacionarem à balística externa como também por serem inteiramente aplicáveis à balística terminal, conforme será demonstrado na terceira parte do estudo.
3 – BALÍSTICA EXTERNA DE CALIBRES DE “ALTA ENERGIA”
Uma vez apresentado o embasamento teórico da balística externa de projéteis propelidos por armas de fogo, vamos agora aplicar tais princípios aos calibres ditos “de alta energia”, sempre trabalhando com os dois “tipos” de calibres apresentados na primeira parte, a saber:
- Calibres de maior velocidade e menor massa, notadamente os calibres de fuzil;
- Calibres de menor velocidade e maior massa.
3.1 – Considerações a respeito do formato dos projéteis
Você já viu anteriormente a importância da forma e massa de um projétil na balística externa. Novamente vamos recorrer aos calibres .223 Remington e .454 Casull apenas para uma comparação mais concreta, sendo possível estender o raciocínio para os demais calibres com as mesmas características. Para ilustrar, vamos observar novamente os formatos dos projéteis desses calibres:

Observando a Figura 6 é possível notar que o formato do projétil de calibre .223 Remington é mais oblongo, consequentemente com coeficiente balístico maior, enquanto que o de calibre .454 Casull é mais “quadrado”, gerando um coeficiente balístico menor. É importante ressaltar que, apesar do coeficiente balístico ser proporcional à massa, o formato do projétil é um fator importante tanto no Coeficiente de Arrasto quanto na área, analisando a Equação 4.
3.2 – Considerações a respeito da velocidade dos projéteis
Observando a Tabela 1 percebe-se que a velocidade do projétil de calibre .223 Remington é de 995 m/s enquanto que a velocidade do projétil de calibre .454 Casull é de 548 m/s. Ambos os projéteis são supersônicos, entretanto a velocidade do primeiro é quase o dobro da velocidade do segundo. Associando esta informação aos coeficientes balísticos de ambos, podemos inferir que isso interfere diretamente na curva balística dos dois calibres, conforme é possível notar na Figura 7.
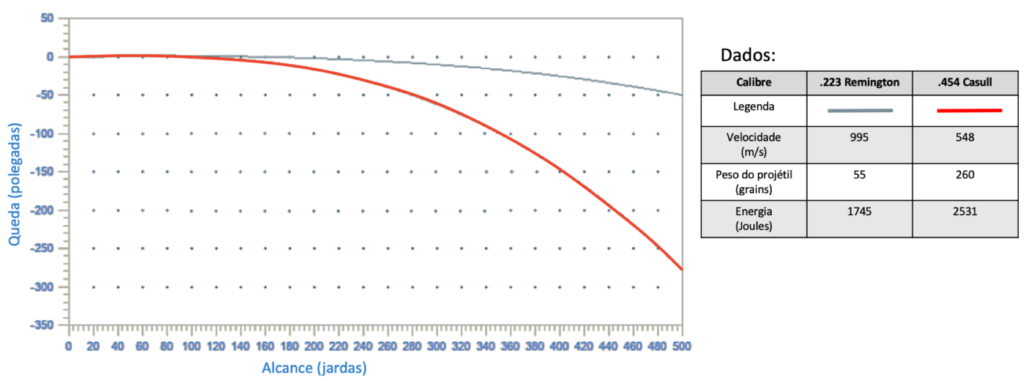
Analisando a Figura 7 é possível perceber que o alcance de projéteis de calibre .454 Casull é sensivelmente inferior ao alcance de projéteis de calibre .223 Remington, apesar da energia ser consideravelmente maior. Além disso, a trajetória do .223 Remington é mais tensa, ou seja, mais aproximada de uma linha reta, do que a trajetória do .454 Casull. Isso se deve tanto à maior velocidade inicial do projétil de calibre .223 Remington, que faz com que ele percorra uma distância maior em um tempo menor, quanto ao seu maior Coeficiente Balístico, que faz com que o projétil consiga ter menor perda de energia cinética por atrito com o ar. Não se esqueça que a energia cinética do calibre .454 Casull é consideravelmente maior que a do calibre .223 Remington! Isso é mais um fator que demonstra que a energia cinética não é um bom parâmetro de comparação de desempenho de calibres.
4 – CONCLUSÃO… AINDA POR ENQUANTO…
Nesta segunda parte do artigo mostramos as diferenças na balística externa dos ditos calibres de “alta energia”, demonstrando que a energia não é um fator preponderante no comportamento dinâmico do projétil. Foi possível perceber que fatores como o formato e velocidade do projétil são muito mais importantes na trajetória do que a energia em si. Na terceira parte do artigo serão analisados os aspectos relacionados à balística terminal desses calibres. Você verá que alguns aspectos abordados na balística externa também são úteis na balística terminal, principalmente nas lesões em tecidos moles. Quem sabe, até lá você já estará convencido em não empregar mais o termo calibres de alta energia e substituirá por calibres de alta velocidade!
BIBLIOGRAFIA
GUNDATA. Gundata. Disponivel em: <http://gundata.org>. Acesso em: 2020 abril 21.
MARIZ, L. G. R. Anotações sobre a doutrina policial: Balística. 1ª Edição. ed. Brasília: Do Autor, v. 2, 2019.
[1]Muitas vezes utilizado erroneamente como sinônimo de massa
[2] Para entender melhor sobre o escoamento laminar e turbulento de fluidos, pesquise sobre o Número de Reynolds.
